关于速度弥散
速度弥散度的定义(velocity dispersion):弥散度是指随机变量方差的平方根,即均方差或标准差。在天文学中﹐速度弥散度通常是指恒星系统中剩余速度的弥散度。下面例举一些天文学中速度弥散的用途:
速度弥散和恒星年龄
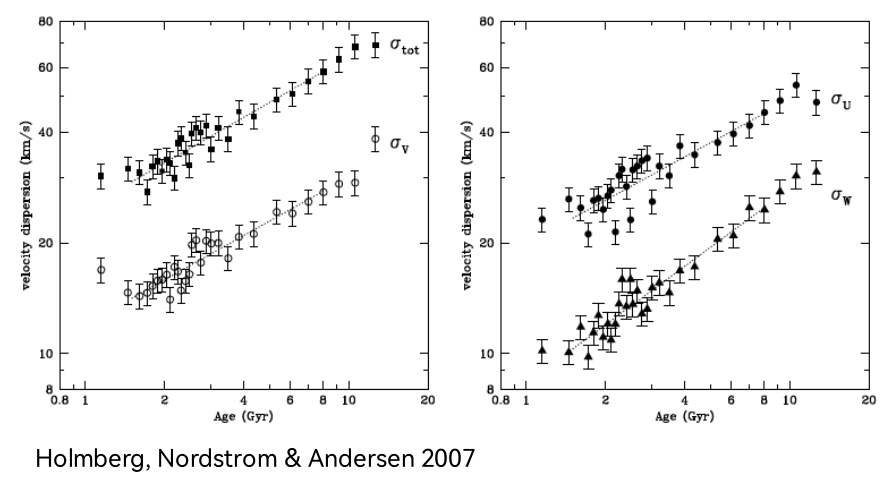
天文统计学研究表明,速度弥散$\sigma$和恒星年龄Age呈相关关系。因此在已知其中一个量的情况下,可以较好的估计另一个量。
Faber-Jackson关系
与盘星系对照,椭圆星系中的恒星并不遵循“有序旋转”,它们的大部分动能投入到了随机运动中,可以用速度弥散描述这种随机运动。Faber-Jackson关系是椭圆星系的光度L与其中发光物质的速度弥散$\sigma$的关系:
也即:
指数$\gamma$接近于4。该关系可以用来测定椭圆星系的距离。
Coma星系团的速度弥散
根据定义编写代码求恒星的弥散速度和速度分布图:
import numpy as np
from astropy.io import fits as pyfits
import astropy.io.fits as fits
import matplotlib
import matplotlib.pyplot as plt
def loadData(filename):
tchfits = fits.open(filename)
tabl = tchfits[1].data.copy()
return tabl
filename = 'ComaCluster.fits'
coma = loadData(filename)
#排除掉红移速度小于0和大于两万的数据,太大的值有可能是背景星:
cz = coma.czA[(coma.czA<20000) & (coma.czA>0)]
sig_cz = np.var(cz)
print(np.sqrt(sig_cz)) #速度弥散
zgrid =np.arange(2000.,12000.,750.)
h, xedge = np.histogram(cz, bins=zgrid)
fig = plt.figure(figsize=[4,4])
ax = fig.add_subplot(111)
print(zgrid)
ax.plot(zgrid[0:-1]+250,h,'k*-') #zgrid的值从第0号取到倒数第二号
ax.set_xlabel('redshift (km/s)')
fig.show()
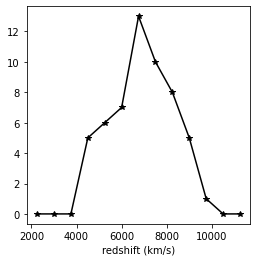
需要注意的是:
1.求速度弥散之前要剔除掉一些离谱的数据:-max_int和redshift超过两万的值,极高redshift值的样本可能是背景星。
2.使用np.histogram根据bins=zgrid划分cz数据点数量的时候,得到的h值的个数比zgrid少一个,所以最后画图的时候横坐标使用zgrid[0:-1]+250。
速度弥散的后验分布
无信息先验分布的正态模型
通常情况下无信息先验分布选择$p(\mu ,ln\sigma)$为均匀分布的正态分布。
这里计算时使用以下步骤的随机抽样方法:
1.先从$\sigma^2|y\sim Inv-\chi^2 (n-1,s^2 )$中抽取随机的$\sigma^{2}$。
1.1数值化实现$Inv-\chi^2$分布:
作为lnv-Gamma分布的一个特例,$\sigma^2 $实际服从变倍的$lnv-\chi^2$分布,即有:
即有:
为了避免计算机处理极大数或极小数的限制,对上式两边同时取对数:
然后减去对数密度分布的最大值:$\bar{z}=z-max\{z\}$
最后再从对数还原为线性值:$p(\theta)=e^{\bar{z}}$
1.2.用python代码还原以上过程:
#使用python
def InvGammaln(x,alpha,beta):
return np.log(beta)*alpha-(special.gammaln(alpha))-\
np.log(x)*(+alpha+1)-beta/x #取对数后的公式,对应公式z=...
#special.gammaln: In(|\Gamma()|)
def Scl_InvChi2ln(x, nu, s2):
return InvGammaln(x, nu/2.,nu/2.*s2)
def randDraw_SInvChi2(nu,s2, N): #从公式抽取随机的sigma2
x = []
k = 0
m = 0
while k<N and m <= 100:
x0 = np.random.uniform(low=1e5,high=10e6,size=N*20)
y0 = np.log(np.random.uniform(\
low=0,high=0.006,size=N*20))
#x0 = logit(x0)
y1 = Scl_InvChi2ln(x0, nu, s2)
ind = (y0<y1)
x.append(x0[ind]) #y0<y1
k = k + np.sum(ind)
m += 1
#print(k,m,len(np.array(x)))
x2 = np.concatenate(x)
xx = np.array(x2).reshape((k,1))
return (xx[0:N])
编写好以上函数后,抽取出的$\sigma^2$可用sigma2 = randDraw_SInvChi2(n-1,s2, N)算出。





